被加熱物が十分大きくて目標温度も700℃以下の鉄でコイルの制約がない場合は80%以上の効率が期待できますが 被加熱物（ワーク）との距離が離れていたり部分加熱などのケースでは一般にロスは50％以上になり、ワークがアルミとなるとロスが70％以上です。

鉄系の場合でも770℃を超えるとキュリー点が有るので急激に効率が落ちます。

物理的にはワークがコイル上で何Ωの抵抗となるかが問題となります。

これは高性能のLCRメーターで測定することが出来ますが、鉄などの磁性体はキュリー点後の値となります。

要するに与えられる電力のうち何％が被加熱物の加熱に関わったかということですが、そもそも回路に大電流を流すわけですから経路に当たる導体部分は当然発熱します、そこで冷却水を流して水冷することになります。

要するに巨大な電気温水器の様です。

この算出結果によりインバーターの容量や用意すべきユーティリティ（電源、冷却水）の大きさを推測します。

抵抗に電流を流せば発熱し発熱は電気的にロスを意味します。

代表的なロス発生箇所に関して検討します。

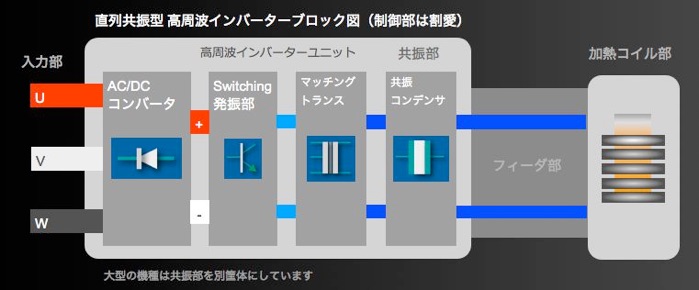
１）フィーダロス

　　高周波電源とコイルを繋げる導体でフィーダとかブスバーと呼ばれています。

　　単純に抵抗分は長さに比例して増加します。

　　極力ロスの小さなフィーダーを考える場合 フィーダーの断面積を大きくする他無いので

　　直列共振回路構成の場合 どうしてもフィーダーが長くなるレイアウトは不向きで

　　マッチング部をコイル側に設置して発振部とマッチング部間のフィーダーを長くする等の工夫が考えられます。

　　つまり 電流が小さい所を長くして電流が大きい所は極力短くするという意味です。

２）コイルロス

　　被加熱物が鉄など比較的抵抗の大きなものであればコイル電流は少なめですが、アルミや銅など抵抗の小さな物を

　　加熱する場合コイル電流が大きくなります。

　　更に加熱箇所や制約からコイルのターン数が得られない場合コイル電流が更に大きくなるので設計が難しくなります。

　　投入電力は電流の二乗✕コイル巻き数で算出しますので4ターンのコイルで加熱できる場合で

　　それを2ターンにしたい場合、電流が√２倍必要になりロスは電流の二乗に比例します。

　　ターン数が減ると同じ共振周波数を得るためにコンデンサ容量が２倍になり耐圧は√２倍高くなるため

　　安易にコイル数を変えるのは大変な事に成ります。

３）共振部、CT（電流トランス）ロス

　　共振部ではマッチングトランスが大きなロスになります。

　　特に周波数が低いと鉄損が多くなり空冷では放熱が間に合わなくなると水冷化します。

　　基本的に周波数が高いとコアが小さくて済むためロスも小さくなります。

　　コンデンサは比較的ロスが少なくて通過電力の0.05％未満ほどです。

　　CTは一次側も大きな電流なので非常に大きなロスが発生します。

全て抵抗なのでロスは電流の増加比の2乗に比例して増えると認識してください。

抵抗の小さな導体の場合は大電流の為に構成部品が大量のロスを発生します。

誘導を使うと非接触で導体に電流を流すことが出来ると加熱原理の項で説明しました。

原理は加熱コイルを使って被加熱物に二次誘導で電流を流すのですが、”熱量の算出”の項で計算したとおりこれには大電流が必要です。

　加熱コイルに高周波電流を流すのですがコイルにはインダクタンス（LH）があり交流では抵抗になります。Zl（Ω） = jωL　ω（角周波数）は２✕π✕ｆ(Hz)なので周波数が高いほど大きくなり、

このままではコイルの抵抗が大きすぎて思うように流れてくれません。

そこでコンデンサを回路に入れて共振回路を作ります。

コンデンサと言っても何百アンペアも流す事のできるコンデンサですから基板に乗っているような小型コンデンサとは種類が違い 物によっては一台数十万円の巨大なコンデンサです。

これで共振回路を作ります。直列共振回路で共振周波数の時、抵抗（インピーダンス）は理論値で0Ωになりこれで交流の大電流が流れるように成ります。

　コイルのインピーダンスが共振により限りなく0Ωになるとコイルに影響を受ける被加熱物の抵抗分がインピーダンスとして回路上に現れてきます。

このインピーダンスに対して適当な電流を流すと結果的に加熱物が電力を消費して発熱します。

　交流の便利な点はトランスを使うと一次側と二次側の比でインピーダンスを変えられる点です。

共振部とコイル側とのインピーダンス整合をとるために高周波トランスを入れます。

インピーダンスが低いと電流がどんどん流れてしまい過負荷になるし高いと高負荷で出力が出ませんので出力に似合ったインピーダンスの整合が必要になります。

このようにアナログ回路ではインピーダンスを合わせこむのにトランスを使用し高周波機器の設計ではマッチングトランスとか出力トランスと呼んでいます。

回路的にはインピーダンスが巻数比で変化します。

　結果的に一次巻線数と二次巻線数の比で二次側に流れる電流が決まります。

例えば３：２の巻数比のトランスは一次側に50A流すと二次側は75A流れています。

それに加熱コイル側の巻数比が効いてきます。

加熱コイルが6ターンなら比加熱物への電流値は450A相当になります。

でも被加熱物の大きさによっては6ターンのコイルに収まらないことも考えられます。

コイルの巻き数が得られない場合はもう一段コイルの前に高周波トランスを追加設置します。

このトランスのことをCT（電流トランス）と呼びます。

（原理、構造は同じですけどこの場合 用途で付けられた名前です。）

さて電流値を稼ぎたい場合はトランス比をどんどん大きくすればいくらでも大電流を得られる様ですがそうは上手く行きません。トランスを経由すると二次側のインダクタンスは巻数比の2乗になってしまいます。周波数を維持したいとするとコイルの巻数が犠牲になります。

常に共振を意識しないとなりません。

被加熱物が鉄系で加熱効率が良ければ概ね80％の効率が得られそうですから

電源は余裕度をみて加熱エネルギーの1.2倍の容量が有れば問題なさそうです。

しかし、アルミや銅など加熱効率が悪い場合は加熱エネルギーの3〜4倍の容量が必要です。

　時々思い違いされることが有るのですが、高周波電源が例えば最大出力50kWの設備を導入して結果的に出力が30kWとなると高周波電源の60％しか使っていないと言われる事が有ります。これは負荷が30kW消費しているだけで高周波電源はその分のエネルギー（電流）が通過しているに過ぎません。丁度ブレーカーの耐圧が50Aで普段30A流れていると言う意味と同等です。

コンデンサを接続しているフィーダの例

トンネル型加熱コルの例

コンデンサブロックの例