物質にエネルギーを与えると加熱して温度が上がります。

これは次の式で算出します。

W = 4.186 ✕ 重量(g) ✕ 比熱(cal) ✕ ⊿温度 / 加熱時間(秒)　.....　式１

本当はJ（ジュール）で表現すべきですがあと電気に置き換えるのでWで表現します。

⊿温度は初期温度、目標温度の差で表します。

⊿温度 = 目標温度 - 初期温度

エネルギーは仕事量の単位W（ワット）です。

掛算と割算の簡単な式で必要なワット数が得られます。

　次にIHの対象となる金属導体でエネルギーを算出してみます。

試しに鉄1kgを20℃から100℃に10秒で加熱したい場合を計算してみます。

W = 4.186 ✕ 1000g ✕ 0.12 ✕ 80℃  / 10　= 4.01856kW

約4kWのエネルギーを10秒与えると20℃の鉄1kgが100℃になる計算です。

掛算と割算だけなのでとっても簡単です。

次にアルミニウムの加熱ではどうでしょうか

同じ重量で同じ目標温度の場合

W = 4.186 ✕ 1000g ✕ 0.214 ✕ 80℃ / 10 = 7.166432kW

7kW強のエネルギーが必要です。

比重の比が3倍位有るので質量（体積）は3倍位に成っています。

加熱したい被加熱物がフィルム状の物や長尺の物を加熱するケースですが

例として鉄板帯板の加熱を考えてみます。

帯板の幅を150mm、厚さ1mmの鉄板（軟鉄）とします。

加熱コイルはトンネル構造で全長を1000mm、帯板の移動速度を20m/minとします。

加熱温度目標は出口100℃、初期温度（入口）は20℃で考えてみます。

これを式１にあてはめるのですが考え方は

コイルと同じ長さの帯板を通過時間相当の時間で加熱すると置き換えます。

まず軟鋼の比重は9.8なのでこれから質量を求めます。

15cm ✕ 0.1cm ✕ 100cm ✕ 9.8 = 1470g

移動時間は速度が毎秒333mmなので1000mmなら3秒です。

これを式１に当てはめます。

W = 4.186 ✕ 1470g ✕ 0.12 ✕ 80℃ / 3 = 19.69kW

20kWのエネルギーを与えれば加熱できそうです。

　金属導体なので電気を使っての加熱を考えます。

鉄とアルミニウムの必要エネルギーを算出したのでこれを電気に置き換えます。

電気による仕事量の計算式は

W = I^2 ✕ r .... 式２

電流の二乗✕抵抗値 です。

電気を流すにあたり形状を定義する必要が有りますが計算しやすいように...

鉄は断面積1cm2で長さを10cmにすると約1kgに成ります。

アルミは同じ断面積なら29cmで約1kgです。

次に形状から抵抗値を算出します。

鉄の場合1cm当たり20μΩなので全長10cmなら200μΩです。

アルミニウムは1cm当たり2.27μΩなので29cmなら65.83μΩになります。

これを式１で求めたエネルギー量を式２に当てはめます。

鉄：4kW = I^2 ✕ 200μΩ　なので　4472Aの電流を流すと10秒で100℃になります。

アルミ：7kW = I^2 ✕ 65.83μΩ　なので　10312Aの電流が必要です。

これは直流の場合で抵抗が小さすぎて実用的では有りません。

加熱原理の項で”表皮効果”を説明しましたがこの物理現象により交流を流すと

遥かに大きな抵抗を得ることが出来ます。

変化量は形状に依存しますが上記の例の場合、鉄は周波数が10kHz程で表面の0.1mmほどまでに狭くなるので抵抗値が100倍くらいに大きくなり上記の計算では450Aの電流で同じエネルギーを与えることが出来る様になります。

物質を個体から液体に変異させる場合融解熱と言う熱エネルギーが必要です。

鉄は1600℃付近で溶解しますがその時融解熱271kJ/kgが別に必要になるので溶解が始まると昇温が停滞します。

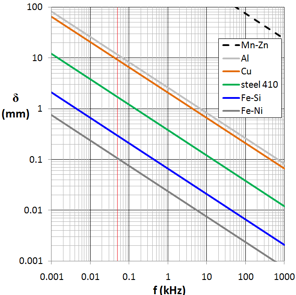
図：１　表皮効果（浸透深さ）

by wikipedia

IH Coil

Unit